Have you ever wondered how to understand complicated data? The Z table can help! It’s a special chart that shows probabilities and helps in statistics. Imagine you’re throwing darts at a target. You want to know where most darts land. Does that sound interesting?
The Z table is like your dartboard. It shows you how far values are from the average or center. This idea is called the “Z-score.” The Z-score tells you how many standard deviations a number is from the mean. Sounds cool, right?
Here’s a fun fact: did you know that this table is used in everyday life? From sports statistics to health studies, the Z table is everywhere! People use it to make decisions based on data. It’s not just for math geeks!
In this article, we’ll explore the Z table and how it works. You’ll learn why it’s important and how you can use it in real-life situations. Ready to dive in and become a data whiz?

Table of Contents
Z Table Explanation: Understanding Z-Scores And Their Use

The Z table helps people understand normal distributions in statistics. It shows the probability of finding a value in a standard normal distribution. With this table, you can quickly find the area under the curve for a given Z score. Imagine scoring 85 on a test; the Z table helps you see how well you did compared to others. Did you know that this simple table is used by scientists, psychologists, and even educators?
What is a Z Table?

Definition of a Z table and its purpose in statistics.. Explanation of how Z tables are used to represent standard normal distribution..
A Z table is a special chart used in statistics. It helps us understand how data spreads out around the average. The main job of a Z table is to show the standard normal distribution. This shows how common certain values are compared to others. For example, a Z score can tell us how far a value is from the average. By looking at a Z table, we can see the percentage of data that falls below that score.
How is the Z table used?
The Z table is used to find probabilities for different data points.
Key uses include:
- Determining how likely a score is.
- Understanding data in various fields like psychology or business.
- Helping in making decisions based on statistical data.
Understanding Z Scores
Definition of Z scores and how they are calculated.. Importance of Z scores in comparing data to a normal distribution..
Z scores are a clever way to see how far a number is from the average. To calculate a Z score, subtract the average from your number and then divide by the standard deviation. Easy peasy! If a Z score is zero, that means your number is sitting right at the average—like a perfect little donut in the middle of a box. This score helps us compare different data points to a normal distribution. If you think of data like a roller coaster, Z scores tell you how high or low you are in relation to the thrill of the ride!
| Term | Definition |
|---|---|
| Z Score | A number showing how far a value is from the mean. |
| Mean | The average of a set of numbers. |
| Standard Deviation | A measure of how spread out the numbers are. |
How to Read a Z Table
Stepbystep guide on interpreting information from a Z table.. Examples of how to find corresponding probabilities for given Z scores..
Reading a Z table is like unlocking a treasure chest of probabilities! First, look for your Z score along the left side. Next, move to the top row to find the second digit. Where these two lines meet shows you the probability. If your Z score is 1.2, find 1.2 in the left column and then look across for the decimal place. Sometimes, it feels like a scavenger hunt, but finding corresponding probabilities is worth the giggles! Want to see how it works? Check this out:
| Z Score | Probability |
|---|---|
| 0.0 | 0.5000 |
| 1.0 | 0.8413 |
| 1.5 | 0.9332 |
| 2.0 | 0.9772 |
So if you have a Z score of 1.5, you’d find that the probability is 0.9332. Easy peasy! Now you’re ready to tackle any Z table like a pro. Happy hunting!
Applications of Z Tables in Real-World Scenarios
Use of Z tables in various fields such as psychology, quality control, and finance.. Case studies showing the practical application of Z tables in data analysis..
Z tables play a big role in many areas. In psychology, they help researchers understand feelings and behaviors by analyzing test scores. In quality control, companies use them to check if products meet certain standards.
Finance experts rely on Z tables to predict market trends, helping them make wiser money choices. Case studies show their impact:
- In a psychology study, a Z table helped analyze student test results, revealing study habits.
- A factory used Z tables to reduce product defects, improving quality.
- Finance analysts used Z tables to forecast stock prices, aiding investment strategies.
These examples illustrate how Z tables guide decisions and improve outcomes in real life.
How are Z tables used in psychology?
Z tables help analyze test scores and understand behaviors effectively.
Key Applications:
- Measuring intelligence.
- Evaluating emotional responses.
Common Misconceptions about Z Tables
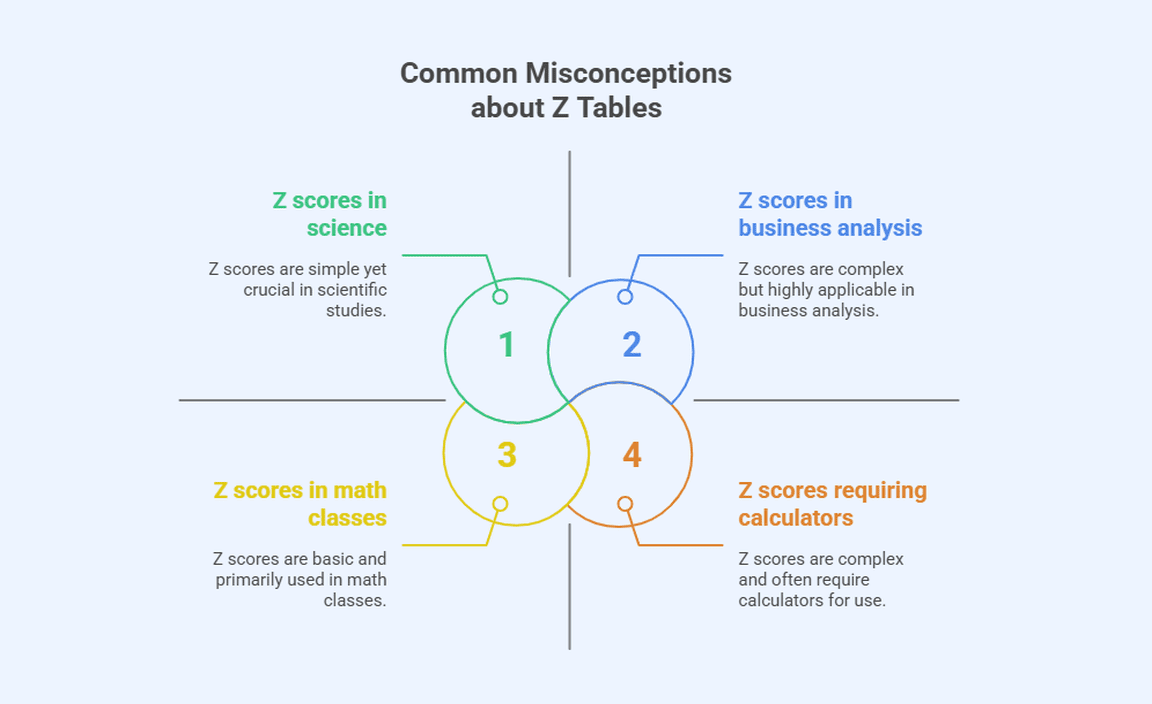
Discussion of frequent misunderstandings related to Z scores and tables.. How to correctly address and overcome these misconceptions..
People often misunderstand z tables. They think z scores are only for math classes. Many do not realize z scores help in areas like business and science. It is crucial to know z tables display probabilities for both sides of the curve. Here are some common myths:
- Z scores can only be positive.
- Z tables are too complicated to use.
- You always need a calculator to find z scores.
To clear these misconceptions, it helps to practice using the z table. Learning can make it seem less scary. Always remember, understanding z tables can open doors for your future!
What is a common misconception about z tables?
Many believe z tables are too complex, making them hesitate to use them.
How to overcome these misconceptions?
Practice with examples and ask questions to build your confidence.
Practice Problems and Examples
Sample problems involving Z scores and Z table usage.. Detailed solutions to each practice problem to reinforce understanding..
Understanding Z scores can be tricky, but practice makes perfect! Let’s tackle some example problems to show how to use the Z table. Say you have a test score of 85, and the class average is 75 with a standard deviation of 10. First, calculate the Z score using the formula: (score – mean) / standard deviation. So, it becomes (85-75)/10 = *1.0*. Next, look up *1.0* in the Z table; you’ll find it gives you a value of *0.8413*. This means about *84.13%* scored below you. Let’s keep it fun with more examples!
| Score | Mean | Standard Deviation | Z Score | Percentile |
|---|---|---|---|---|
| 85 | 75 | 10 | 1.0 | *84.13%* |
| 90 | 75 | 10 | 1.5 | *93.32%* |
In the next problem, if a score of 90 gives a Z score of *1.5*, the Z table shows *93.32%* scored lower. So, you’d own that classroom! Keep practicing, and soon you’ll be a Z score master!
Tips for Using Z Tables Effectively
Strategies for quick access and calculations using Z tables.. Tools and resources that can enhance the use of Z tables in research..
Using Z tables can be like finding treasure if you have the right tools. First, keep a calculator handy for quick math. Make sure to have a cheat sheet for common Z values so you don’t waste time searching. You can find plenty of online resources that can simplify your calculations. Using software like Excel can also speed things up!
| Tool | Purpose |
|---|---|
| Calculator | Quick calculations |
| Cheat Sheet | Common Z values |
| Online Resources | Guidance and formulas |
| Excel | Speedy analysis |
These strategies will not only save you time but might even help you impress your friends. After all, who doesn’t love a good math joke? Why did the student bring a ladder to class? Because they wanted to go to high school!
Conclusion
In conclusion, the Z table helps you understand how data is spread in a normal curve. It shows probabilities for different values. You can use it to find percentages related to statistics. To improve your skills, practice with Z scores and real examples. Keep reading about statistics to become more confident in using the Z table!
FAQs
What Is A Z Table, And How Is It Used In Statistical Analysis?
A Z table helps us understand how numbers are spread out. It shows the area or chance of getting a score in a normal curve. We use it when we want to find out how unusual or common a score is. For example, if we have a test score, we can see how it compares to other scores. This helps us make better decisions based on the data.
How Do You Interpret The Values Found In A Z Table?
A Z table helps us understand how far a number is from the average. Each value in the table tells you how many people score lower than a certain number. If you see a higher number, it means it’s less common. If it’s lower, it means more people have that score. We use this table to see how special or ordinary a score is.
What Is The Significance Of The Mean And Standard Deviation In Relation To A Z Table?
The mean is like the average score in a game, showing what we expect. The standard deviation tells us how much scores differ from that average. A Z table helps us see how far a score is from the mean. It uses these two numbers to help us understand how likely certain scores are. This way, we can make smarter guesses about scores and chances.
How Can You Calculate A Z Score, And How Does It Relate To The Values In A Z Table?
To calculate a Z score, you need three things: the number you have, the average of the group, and how spread out the group is. First, subtract the average from your number. Then, divide that result by how spread out the group is. The Z score tells you how far your number is from the average. We can find out what this means by looking at a Z table, which shows how common or rare different Z scores are.
What Are The Differences Between A Standard Normal Distribution And Other Types Of Distributions When Using A Z Table?
A standard normal distribution is special because it has a mean of 0 and a standard deviation of 1. Other types of distributions can have different means and spread out differently. When we use a Z table, we find how far a score is from the mean in standard normal distribution. For other distributions, we often need to change them to standard normal to use the Z table. This helps us understand how likely something is to happen.
Understanding Standard Deviation Clearly: https://www.investopedia.com/terms/s/standarddeviation.asp
Real-Life Examples of Data Analysis: https://www.scribbr.com/statistics/descriptive-statistics/
Z Score and Probability Basics: https://stattrek.com/statistics/normal-distribution.aspx
How Excel Can Help With Z Scores: https://support.microsoft.com/en-us/office/z-test-function-5932f0c0-60d3-4f34-80da-6c4b904e017b






